
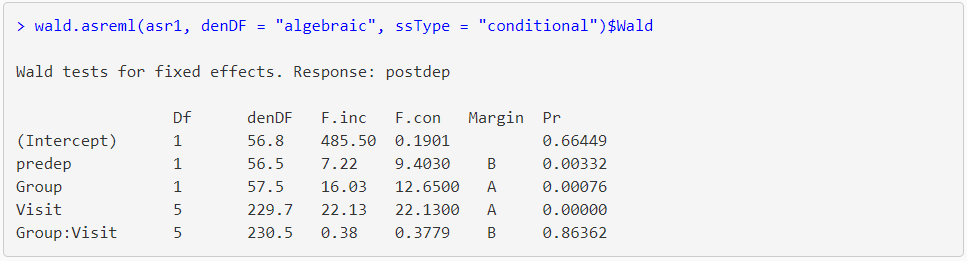
(In a multi-factor experiment, it may still be reasonable to construct some marginal means where we are averaging only over negligible interaction effects). If, on the other hand, we do have sizeable interaction effects, then (as our forebears recommend) we simply should not even consider estimating marginal means. They mimic the types of analyses proposed for balanced experiments by the giants among our forebears. Is this useful? Definitely yes, when the model is additive and/or the interaction effects are small. And the ideas can be applied to Bayesian models fitted via MCMC methods, simply by computing the relevant quantities from the posterior predictions. You can also generalize these ideas to experimental data analyzed with other types of models, including generalized linear models, ordinal models and multinomial models, zero-inflated models, etc. The idea extends to other experimental designs, such as Latin squares, split-plots, etc., and even to covariance models (where typically we make predictions at the mean of each covariate). But these LS means are linear functions of the model predictions, and hence of the regression coefficients so they can be estimated from the model with no need for ad hoc quantities like $\tilde n$.
$$ Y_$ then our marginal means are estimated as equally-weighted marginal averages of these predictions, just as in unweighted-means analysis.

For that, we randomize experimental units to combinations of the levels of two factors $A$ and $B$, and consider analyzing a model of the form Then they move on to factorial designs, and it is a 2-way factorial I will discuss the most. Such a book has initial chapters on one-way CRDs, focusing especially on balanced designs.
Look at a standard experimental design textbook - pretty much any of them.
The underlying ideas are very old (and predate SAS by at least 50 years). The short answer is that LS means (or more modernly, estimated marginal means) are incredibly useful with experimental data.


 0 kommentar(er)
0 kommentar(er)
